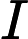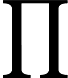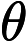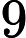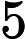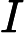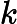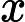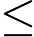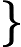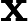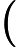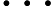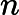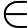Consecuencias de la desigualdad de correlación gaussiana para calcular intervalos de confianza conjuntos

Según este artículo muy interesante en la revista Quanta: "Una prueba largamente buscada, encontrada y casi perdida" , se ha demostrado que dado un vector tiene una distribución gaussiana multivariante, y dados los intervalos centrado alrededor de las medias de los componentes correspondientes de , entonces $\mathbf{x}=(x_1,\dots,x_n)$ $I_1,\dots,I_n$ $\mathbf{x}$

p (x_{1} \in I_{1}, \dots, x_{n} \in I_{n}) \geq \prod_{i = 1}^{n} p (x_{i} \in I_{i})

$p(x_1\in I_1, \dots, x_n\in I_n)\geq \prod_{i=1}^n p(x_i\in I_i)$

(Desigualdad de correlación gaussiana o GCI; consulte https://arxiv.org/pdf/1512.08776.pdf para obtener una formulación más general).

Esto parece realmente agradable y simple, y el artículo dice que tiene consecuencias para los intervalos de confianza conjunta. Sin embargo, me parece bastante inútil a ese respecto. Supongamos que estamos estimando los parámetros , y encontramos estimadores que son (tal vez asintóticamente) conjuntamente normales (por ejemplo, el estimador MLE). Luego, si calculo intervalos de confianza del 95% para cada parámetro, el GCI garantiza que el hipercubo es una región de confianza conjunta con una cobertura no menor que $\theta_1,\dots,\theta_n$ $\hat{\theta_1},\dots,\hat{\theta_n}$ $I_1\times\dots I_n$ ... que es una cobertura bastante baja incluso para moderado. $(0.95)^n$ $n$

Por lo tanto, no parece una forma inteligente de encontrar regiones de confianza conjuntas: la región de confianza habitual para un gaussiano multivariado, es decir, un hiperelipsoide, no es difícil de encontrar si se conoce la matriz de covarianza y es más nítida. ¿Quizás podría ser útil encontrar regiones de confianza cuando se desconoce la matriz de covarianza? ¿Me puede mostrar un ejemplo de la relevancia de GCI para el cálculo de las regiones de confianza conjunta?

normal-distribution confidence-interval multivariate-normal

— DeltaIV
fuente

Tienes la idea correcta. Los intervalos de confianza individuales deben ser muy superiores al 95% para que la región conjunta alcance el 95%. Cada uno debe ser al menos 0,95 elevado a la 1ª potencia.

— Michael R. Chernick

I_{k}

$I_k$

I_{k} = {x : | x | \leq x_{k}}

$I_k=\{x: |x|\leq x_k\}$

@amoeba No me preocupa la dificultad de la prueba, sino su relevancia para las estadísticas aplicadas. Si considerar un hiperrectángulo hace que sea más fácil mostrar tal relevancia, bien. Si, en cambio, cree que esta desigualdad solo se vuelve útil en la práctica cuando se considera un polígono arbitrario, lo suficientemente justo. Aceptaré una respuesta que diga "si considera solo hiperrectángulos, GCI no es una herramienta muy útil para un estadístico aplicado, porque ... Pero si considera polígonos arbitrarios, entonces se vuelve relevante, porque ..."

— DeltaIV

Quería editar y busqué en los documentos las pruebas, pero ahora ya no estoy 100% seguro si el hiperrectángulo es un caso especial / fácil o una formulación equivalente. Lo dejaré por ahora y tal vez vuelva aquí más tarde.

— ameba dice Reinstate Monica

H

$H$

x = (x_{1}, \dots, x_{n}) \in H ⟺ - x \in H

$\mathbf{x}=(x_1,\dots,x_n)\in H \iff -\mathbf{x} \in H$

Creo que la pregunta es más relevante. En cierto sentido, usted está mirando múltiples pruebas de hipótesis y comparándolas con la ejecución de múltiples pruebas de hipótesis.

Sí, de hecho hay un límite inferior que es el producto de los valores p de las pruebas que suponen independencia. Esta es la base para los ajustes de los valores p en las pruebas de hipótesis múltiples, como los ajustes de Bonferroni o Holm. Pero los ajustes de Bonferroni y Holm (suponiendo independencia) son pruebas de potencia particularmente baja.

Se puede hacer mucho mejor en la práctica (y esto se hace a través de Bootstrap, ver, por ejemplo, H White's Bootstrap Reality Check, los documentos de Romano-Wolf y el conjunto más reciente de documentos sobre Conjuntos de confianza del modelo). Cada uno de estos es un intento de una prueba de hipótesis de mayor potencia (por ejemplo, usar la correlación estimada para hacerlo mejor que simplemente usar este límite inferior) y, en consecuencia, mucho más relevante.

— NBF
fuente