¿Cuáles son las ideas principales, es decir, los conceptos relacionados con el teorema de Bayes ? No estoy pidiendo derivaciones de notación matemática compleja.
¿De qué se trata el teorema de Bayes?
Respuestas:
El teorema de Bayes es un resultado relativamente simple, pero fundamental de la teoría de probabilidad que permite el cálculo de ciertas probabilidades condicionales. Las probabilidades condicionales son solo aquellas probabilidades que reflejan la influencia de un evento en la probabilidad de otro.
En pocas palabras, en su forma más famosa, establece que la probabilidad de una hipótesis dada los nuevos datos ( P (H | D) ; llamada probabilidad posterior) es igual a la siguiente ecuación: la probabilidad de los datos observados dada la hipótesis ( P (D | H) ; llamada probabilidad condicional), multiplicada por la probabilidad de que la teoría sea verdadera antes de la nueva evidencia ( P (H) ; llamada probabilidad previa de H), dividida por la probabilidad de ver esos datos, punto ( P (D ); llamado la probabilidad marginal de D).
Formalmente, la ecuación se ve así:
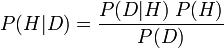
La importancia del teorema de Bayes se debe en gran medida a que su uso adecuado es un punto de discusión entre las escuelas de pensamiento sobre la probabilidad. Para un Bayesiano subjetivo (que interpreta la probabilidad como grados subjetivos de creencia), el teorema de Bayes proporciona la piedra angular para la prueba de la teoría, la selección de la teoría y otras prácticas, al conectar sus juicios de probabilidad subjetiva en la ecuación y ejecutarla. Para un frecuentista (que interpreta la probabilidad como frecuencias relativas limitantes ), este uso del teorema de Bayes es un abuso, y en su lugar se esfuerzan por usar antecedentes significativos (no subjetivos) (al igual que los bayesianos objetivos bajo otra interpretación de la probabilidad).
Lo siento, pero parece haber cierta confusión aquí: el teorema de Bayes no está en discusión sobre el interminable Bayesiano. Frequentist debate. Es un teorema que es consistente con ambas escuelas de pensamiento (dado que es consistente con los axiomas de probabilidad de Kolmogorov).
Por supuesto, el teorema de Bayes es el núcleo de las estadísticas bayesianas, pero el teorema en sí es universal. El choque entre los frecuentistas y los bayesianos se debe principalmente a cómo se pueden definir o no las distribuciones anteriores.
Entonces, si la pregunta es sobre el teorema de Bayes (y no las estadísticas bayesianas):
El teorema de Bayes define cómo se pueden calcular las probabilidades condicionales específicas. Imagine, por ejemplo, que sabe: la probabilidad de que alguien tenga el síntoma A, dado que tiene la enfermedad X p (A | X); la probabilidad de que alguien en general tenga la enfermedad X p (X); La probabilidad de que alguien en general tenga el síntoma A p (A). con estos 3 datos puede calcular la probabilidad de que alguien tenga la enfermedad X, dado que tiene el síntoma A p (X | A).
Puede derivar el teorema de Bayes usted mismo de la siguiente manera. Comience con la definición de razón de una probabilidad condicional:
Now to slot this into the formula for , just rewrite the formula above so is on the left:
and hey presto:
As for what the point is to rotating a conditional probability in this way, consider the common example of trying to infer the probability that someone has a disease given that they have a symptom, i.e., we know that they have a symptom - we can just see it - but we cannot be certain whether they have a disease and have to infer it. I'll start with the formula and work back.
So to work it out, you need to know the prior probability of the symptom, the prior probability of the disease (i.e., how common or rare are the symptom and disease) and also the probability that someone has a symptom given we know someone has a disease (e.g., via expensive time consuming lab tests).
It can get a lot more complicated than this, e.g., if you have multiple diseases and symptoms, but the idea is the same. Even more generally, Bayes' theorem often makes an appearance if you have a probability theory of relationships between causes (e.g., diseases) and effects (e.g., symptoms) and you need to reason backwards (e.g., you see some symptoms from which you want to infer the underlying disease).
There are two main schools of thought is Statistics: frequentist and Bayesian.
Bayes theorem is to do with the latter and can be seen as a way of understanding how the probability that a theory is true is affected by a new piece of evidence. This is known as conditional probability. You might want to look at this to get a handle on the math.
Let me give you a very very intuitional insight. Suppose you are tossing a coin 10 times and you get 8 heads and 2 tails. The question that would come to your mind is whether this coin is biased towards heads or not.
Now if you go by conventional definitions or the frequentist approach of probability you might say that the coin is unbiased and this is an exceptional occurrence. Hence you would conclude that the possibility of getting a head next toss is also 50%.
But suppose you are a Bayesian. You would actually think that since you have got exceptionally high number of heads, the coin has a bias towards the head side. There are methods to calculate this possible bias. You would calculate them and then when you toss the coin next time, you would definitely call a heads.
So, Bayesian probability is about the belief that you develop based on the data you observe. I hope that was simple enough.
Bayes' theorem relates two ideas: probability and likelihood. Probability says: given this model, these are the outcomes. So: given a fair coin, I'll get heads 50% of the time. Likelihood says: given these outcomes, this is what we can say about the model. So: if you toss a coin 100 times and get 88 heads (to pick up on a previous example and make it more extreme), then the likelihood that the fair coin model is correct is not so high.
One of the standard examples used to illustrate Bayes' theorem is the idea of testing for a disease: if you take a test that's 95% accurate for a disease that 1 in 10000 of the population have, and you test positive, what are the chances that you have the disease?
The naive answer is 95%, but this ignores the issue that 5% of the tests on 9999 out of 10000 people will give a false positive. So your odds of having the disease are far lower than 95%.
My use of the vague phrase "what are the chances" is deliberate. To use the probability/likelihood language: the probability that the test is accurate is 95%, but what you want to know is the likelihood that you have the disease.
Slightly off topic: The other classic example which Bayes theorem is used to solve in all the textbooks is the Monty Hall problem: You're on a quiz show. There is a prize behind one of three doors. You choose door one. The host opens door three to reveal no prize. Should you change to door two given the chance?
I like the rewording of the question (courtesy of the reference below): you're on a quiz show. There is a prize behind one of a million doors. You choose door one. The host opens all the other doors except door 104632 to reveal no prize. Should you change to door 104632?
My favourite book which discusses Bayes' theorem, very much from the Bayesian perspective, is "Information Theory, Inference and Learning Algorithms ", by David J. C. MacKay. It's a Cambridge University Press book, ISBN-13: 9780521642989. My answer is (I hope) a distillation of the kind of discussions made in the book. (Usual rules apply: I have no affiliations with the author, I just like the book).
Bayes theorem in its most obvious form is simply a re-statement of two things:
- the joint probability is symmetric in its arguments
- the product rule
So by using the symmetry:
Now if you can divide both sides by to get:
So this is it? How can something so simple be so awesome? As with most things "its the journey that's more important than the destination". Bayes theorem rocks because of the arguments that lead to it.
What is missing from this is that the product rule and sum rule , can be derived using deductive logic based on axioms of consistent reasoning.
Now the "rule" in deductive logic is that if you have a relationship "A implies B" then you also have "Not B implies Not A". So we have "consistent reasoning implies Bayes theorem". This means "Not Bayes theorem implies Not consistent reasoning". i.e. if your result isn't equivalent to a Bayesian result for some prior and likelihood then you are reasoning inconsistently.
This result is called Cox's theorem and was proved in "Algebra of Probable inference" in the 1940's. A more recent derivation is given in Proability theory: The logic of science.
I really like Kevin Murphy's intro the to Bayes Theorem http://www.cs.ubc.ca/~murphyk/Bayes/bayesrule.html
The quote here is from an economist article:
http://www.cs.ubc.ca/~murphyk/Bayes/economist.html
The essence of the Bayesian approach is to provide a mathematical rule explaining how you should change your existing beliefs in the light of new evidence. In other words, it allows scientists to combine new data with their existing knowledge or expertise. The canonical example is to imagine that a precocious newborn observes his first sunset, and wonders whether the sun will rise again or not. He assigns equal prior probabilities to both possible outcomes, and represents this by placing one white and one black marble into a bag. The following day, when the sun rises, the child places another white marble in the bag. The probability that a marble plucked randomly from the bag will be white (ie, the child's degree of belief in future sunrises) has thus gone from a half to two-thirds. After sunrise the next day, the child adds another white marble, and the probability (and thus the degree of belief) goes from two-thirds to three-quarters. And so on. Gradually, the initial belief that the sun is just as likely as not to rise each morning is modified to become a near-certainty that the sun will always rise.