Como señalan los comentarios a su pregunta, hay muchas personas trabajando para encontrar algo mejor. Sin embargo, me gustaría responder a esta pregunta ampliando el comentario dejado por @josh
Todos los modelos están equivocados pero algunos son útiles (Wiki)
La afirmación anterior es una verdad general utilizada para describir la naturaleza de los modelos estadísticos. Con los datos que tenemos disponibles, podemos crear modelos que nos permitan hacer cosas útiles, como aproximar un valor pronosticado.
Tomemos por ejemplo la regresión lineal
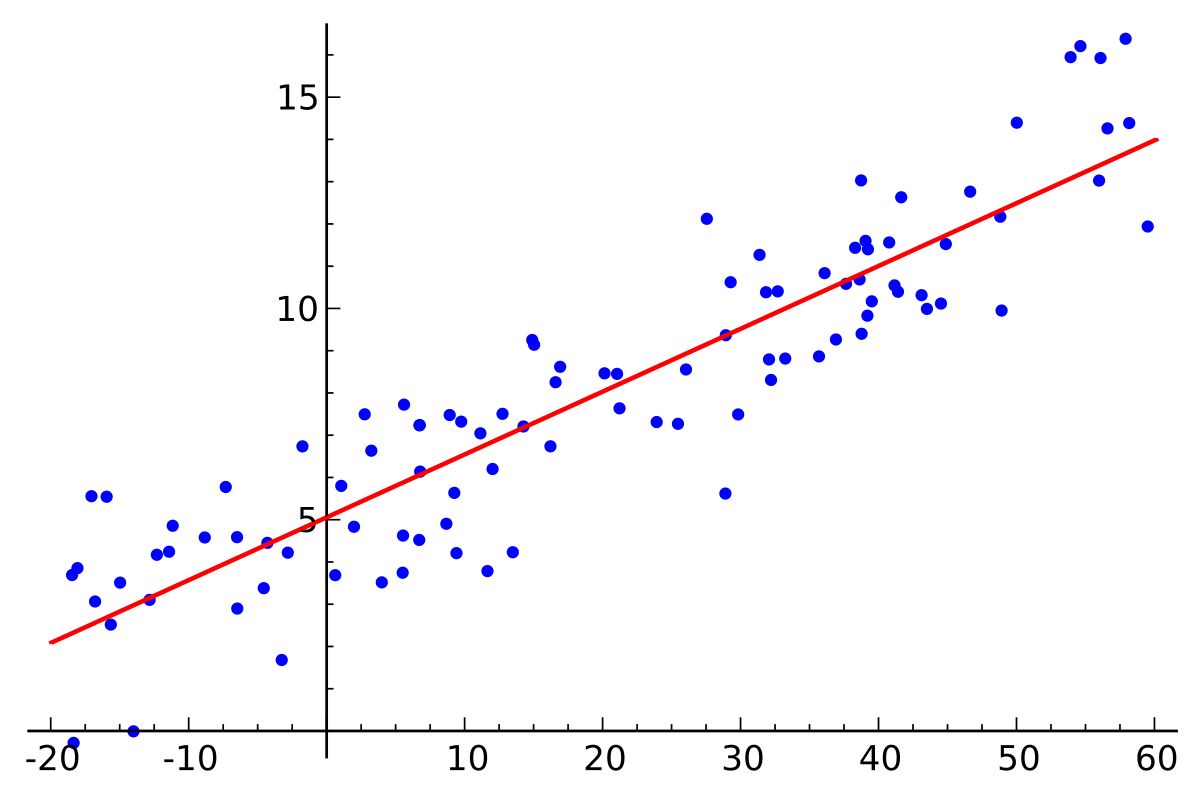
Usando una serie de observaciones, podemos ajustar un modelo para darnos un valor aproximado para una variable dependiente dado cualquier valor para la variable o variables independientes.
Burnham, KP; Anderson, DR (2002), Model Selection and Multimodel> Inference: A Practical Information-Theoretic Approach (2nd ed.):
"Un modelo es una simplificación o aproximación de la realidad y, por lo tanto, no reflejará toda la realidad ... Box señaló que" todos los modelos están equivocados, pero algunos son útiles ". Si bien un modelo nunca puede ser" verdad ", un modelo podría ser clasificado de muy útil, a útil, a algo útil para, finalmente, esencialmente inútil ".
Las desviaciones de nuestro modelo (como se puede ver en la imagen de arriba) aparecen al azar, algunas observaciones están debajo de la línea y otras arriba, pero nuestra línea de regresión muestra una correlación general. Si bien las desviaciones en nuestro modelo parecen aleatorias, en escenarios realistas habrá otros factores en juego que causen esta desviación. Por ejemplo, imagine ver autos mientras conducen a través de un cruce donde deben girar a la izquierda o derecha para continuar, los autos no giran en ningún patrón en particular. Si bien podríamos decir que la dirección en la que giran los autos es completamente aleatoria, ¿llega cada conductor al cruce y en ese punto toma una decisión aleatoria sobre qué camino tomar? En realidad, probablemente se dirigen a un lugar específico por una razón específica, y sin intentar detener cada auto para preguntarles sobre su razonamiento, solo podemos describir sus acciones como aleatorias.
Cuando podamos ajustar un modelo con una desviación mínima, ¿qué tan seguros podemos estar de que una variable desconocida, inadvertida o inconmensurable no arrojará en algún momento nuestro modelo? ¿La aleta de las alas de una mariposa en Brasil desencadenó un tornado en Texas?
El problema con el uso de los modelos Lineal y SVN que usted menciona solo es que estamos obligados a observar manualmente nuestras variables y cómo se afectan entre sí. Luego necesitamos decidir qué variables son importantes y escribir un algoritmo específico de la tarea. Esto puede ser sencillo si solo tenemos unas pocas variables, pero ¿y si tuviéramos miles? ¿Qué pasaría si quisiéramos crear un modelo generalizado de reconocimiento de imágenes, podría lograrse esto de manera realista con este enfoque?
El aprendizaje profundo y las redes neuronales artificiales (ANN) pueden ayudarnos a crear modelos útiles para grandes conjuntos de datos que contienen grandes cantidades de variables (por ejemplo, bibliotecas de imágenes). Como mencionas, hay una cantidad incomprensible de soluciones que podrían ajustarse a los datos usando ANN, pero ¿es esta cifra realmente diferente a la cantidad de soluciones que necesitaríamos desarrollar a través de prueba y error?
La aplicación de ANN hace gran parte del trabajo por nosotros, podemos especificar nuestras entradas y nuestros resultados deseados (y ajustarlos más tarde para realizar mejoras) y dejar que ANN dependa de la solución. Esta es la razón por la cual las ANN a menudo se describen como "cajas negras" . A partir de una entrada dada, generan una aproximación, sin embargo (en términos generales) estas aproximaciones no incluyen detalles sobre cómo se aproximaron.
Entonces, realmente se reduce a qué problema está tratando de resolver, ya que el problema determinará qué enfoque modelo es más útil. Los modelos no son absolutamente precisos, por lo que siempre hay un elemento de estar 'equivocado'; sin embargo, cuanto más precisos sean los resultados, más útiles serán. Tener más detalles en los resultados sobre cómo se hizo la aproximación también puede ser útil, dependiendo del problema, incluso puede ser más útil que una mayor precisión.
Si, por ejemplo, está calculando el puntaje de crédito de una persona, el uso de regresión y SVM proporciona cálculos que pueden explorarse mejor. Es muy útil poder ajustar el modelo directamente y explicar a los clientes el efecto que tienen las variables independientes separadas en su puntaje general. Un ANN puede ayudar en el procesamiento de grandes cantidades de variables para lograr una puntuación más precisa, pero ¿sería más útil esta precisión?
