Suponiendo que las variables son positivas o no negativas, los bordes del borde son solo puntos más allá de los cuales los datos serían 0 o negativos, respectivamente. Como tales datos de la vida real tienden a estar sesgados, vemos una mayor densidad de puntos en el extremo inferior de su distribución y, por lo tanto, una mayor densidad en el "punto" de la cuña.
En términos más generales, PCA es simplemente una rotación de los datos y las restricciones sobre esos datos generalmente serán visibles en los componentes principales de la misma manera que se muestra en la pregunta.
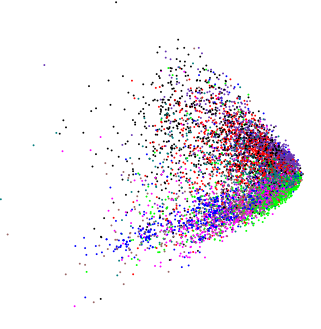
Aquí hay un ejemplo que usa varias variables log-normalmente distribuidas:
library("vegan")
set.seed(1)
df <- data.frame(matrix(rlnorm(5*10000), ncol = 5))
plot(rda(df), display = "sites")

Dependiendo de la rotación implicada por las dos primeras PC, es posible que vea la cuña o que vea una versión algo diferente, que se muestra aquí en 3D usando ( ordirgl()en lugar de plot())

Aquí, en 3d, vemos múltiples picos que sobresalen de la masa central.
Xi∼(N)(μ=0,σ=1)
set.seed(1)
df2 <- data.frame(matrix(rnorm(5*10000), ncol = 5))
plot(rda(df2), display = "sites")


Y para variables aleatorias positivas uniformes vemos un cubo
set.seed(1)
df3 <- data.frame(matrix(runif(3*10000), ncol = 3))
plot(rda(df3), display = "sites")


Tenga en cuenta que aquí, para la ilustración, muestro el uniforme usando solo 3 variables aleatorias, por lo tanto, los puntos describen un cubo en 3d. Con dimensiones más altas / más variables no podemos representar el hipercubo 5d perfectamente en 3d y, por lo tanto, la forma distintiva del "cubo" se distorsiona un poco. Problemas similares afectan los otros ejemplos mostrados, pero aún es fácil ver las restricciones en esos ejemplos.
Para sus datos, una transformación logarítmica de las variables antes de PCA tiraría de las colas y estiraría los datos agrupados, tal como podría usar dicha transformación en una regresión lineal.
Otras formas pueden surgir en parcelas PCA; Una de esas formas es un artefacto de la representación métrica conservada en el PCA y se conoce como la herradura . Para datos con un gradiente largo o dominante (se sabe que las muestras ordenadas a lo largo de una sola dimensión con variables que aumentan de 0 a un máximo y luego disminuyen nuevamente a 0 a lo largo de porciones de datos generan estos artefactos).
ll <- data.frame(Species1 = c(1,2,4,7,8,7,4,2,1,rep(0,10)),
Species2 = c(rep(0, 5),1,2,4,7,8,7,4,2,1, rep(0, 5)),
Species3 = c(rep(0, 10),1,2,4,7,8,7,4,2,1))
rownames(ll) <- paste0("site", seq_len(NROW(ll)))
matplot(ll, type = "o", col = 1:3, pch = 21:23, bg = 1:3,
ylab = "Abundance", xlab = "Sites")

que produce una herradura extrema, donde los puntos en los extremos de los ejes se doblan hacia el centro.

 .
. (excepto en este caso, realmente quería saber si hay alguna estructura interna).
(excepto en este caso, realmente quería saber si hay alguna estructura interna).






