Estoy tratando de hacer una esfera cuádruple basada en un artículo , que muestra resultados como este:
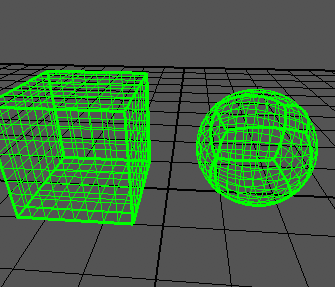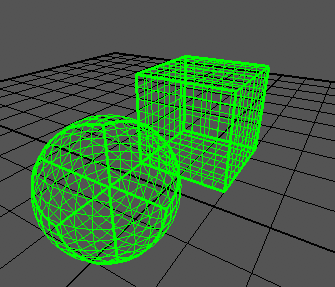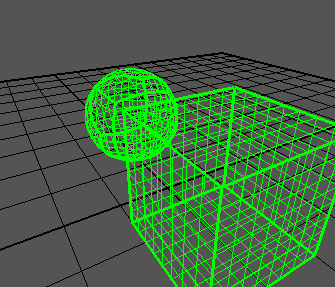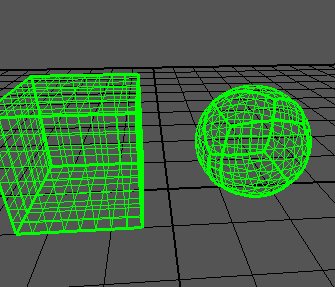
Puedo generar un cubo correctamente:

Pero cuando convierto todos los puntos de acuerdo con esta fórmula (de la página vinculada anteriormente):
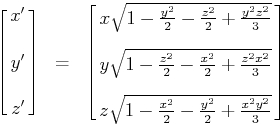
x = x * sqrtf(1.0 - (y*y/2.0) - (z*z/2.0) + (y*y*z*z/3.0));
y = y * sqrtf(1.0 - (z*z/2.0) - (x*x/2.0) + (z*z*x*x/3.0));
z = z * sqrtf(1.0 - (x*x/2.0) - (y*y/2.0) + (x*x*y*y/3.0));Mi esfera se ve así:

Como puede ver, los bordes del cubo todavía sobresalen demasiado. El cubo varía de -1a +1en todos los ejes, como dice el artículo.
¿Alguna idea de lo que está mal?
1
¿Su implementación contiene el problema "x = x ..." también o es solo aquí?
—
serpiente5
Fantásticas ayudas visuales. Gracias por incluirlos.
—
doppelgreener
Para responder la pregunta en el título, puede normalizar los vértices del cubo para convertirlo en una esfera. Sin embargo, la distribución de los vértices probablemente será diferente del método vinculado.
—
msell
Relacionado: gamedev.stackexchange.com/questions/7189/…
—
MichaelHouse