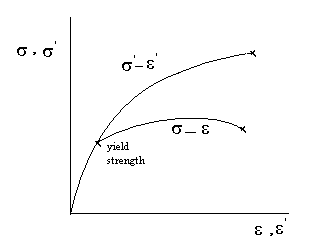Usamos la deformación de ingeniería a pesar de que no es el valor "correcto" porque en la mayoría de los casos, específicamente en el régimen elástico, la deformación de ingeniería difiere insignificantemente de la deformación verdadera.
Para materiales Hookean elásticos lineales, generalmente la tensión del caso en el límite elástico es muy pequeña. Incluso los aceros más fuertes, por ejemplo, tienen un límite superior cuando se trabaja en frío de aproximadamente . El módulo de acero es aproximadamente . Por lo tanto, para los aceros más fuertes. Entonces, al comienzo de la deformación plástica, la deformación de ingeniería es . Muchos materiales elásticos útiles tienen una tensión de ingeniería mucho menor en sus límites elásticos. E = 200 × 10 9 Pa ε el = 0.005 = 0.5 % 0.5 %σel= 1 × 109 9 Pensilvaniami= 200 × 109 9 Pensilvaniaεel= 0.005 = 0.5 %0.5 %
Para un sólido isotrópico, elástico de Hookean, lo siguiente es cierto
εX1= 1mi[ σX1- ν( σX2+ σX3) ]
sin pérdida de generalidad en la elección de . Entonces, en tensión uniaxial en el límite elástico, asumiendo que el material es libre de contraerse. Así . Dado que la relación de Poisson es aproximadamente 0.3 para aceros en el régimen elástico, la deformación por compresión lineal de sección transversal es . El área de la sección transversal en el límite elástico es , o muy cercana a veces el área original.XyoσX2= σX3= 0εX2= εX3= - σelνmi= - νεelν0.0015( 1 - 0.0015 )2UN0 00,997
10,9971.0030,3%
Si bien el análisis anterior es razonablemente útil para sólidos Hookean linealmente elásticos, no es tan bueno para polímeros y materiales biológicos. Dichos materiales suelen ser viscoelásticos (u otra clase de material por completo) y, por lo tanto, obedecen a diferentes reglas en su comportamiento. La tensión verdadera también difiere bastante de la tensión de ingeniería en el régimen plástico, como se evidencia en la siguiente gráfica (que se encuentra aquí )
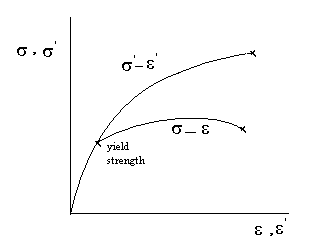
En cuanto a sus puntos:
Medir los cambios en el área de la sección transversal durante la deformación es difícil. Requiere la colocación cuidadosa de instrumentación calibrada en muestras de prueba mecanizadas con precisión. Se podrían utilizar medidores de tensión colocados a los lados de una barra de tensión para medir la tensión lateral en tensión uniaxial y compresión en equipos de prueba de tracción . La obtención de resultados estadísticamente significativos toma muchas muestras, así como un tiempo, esfuerzo y costo significativos.
0.3 %
La idea de que podemos ignorar cualquier cosa más allá del final del régimen elástico, o que siempre diseñamos para el régimen elástico, no es cierta. La deformación plástica a menudo puede valer la pena estudiar. El modelado de procesos continuos de formación de formas, como rodar, dibujar, extruir, etc. requiere una comprensión profunda de la mecánica de la deformación plástica para funcionar con éxito, y para ese fin, el verdadero esfuerzo y la verdadera tensión son invaluables. Específicamente para el trefilado, vea (este pdf ) y encuentre la ecuación 7. La deformación plástica también es útil para modelar materiales que deben deformarse permanentemente en algunos casos de uso esperados, como los paneles de la carrocería del automóvil y los componentes del marco durante una colisión. La deformación plástica es útil porque absorbe energía cinética.
Editar: Pido disculpas, en realidad no respondí la pregunta por estrés. Sin embargo, debe quedar bastante claro que los mismos puntos se aplican al estrés como a la tensión dada su relación lineal en el régimen elástico. Nuevamente, en el régimen plástico, puede haber grandes variaciones.