¿Se puede evitar el paso de "división" en una fusión?

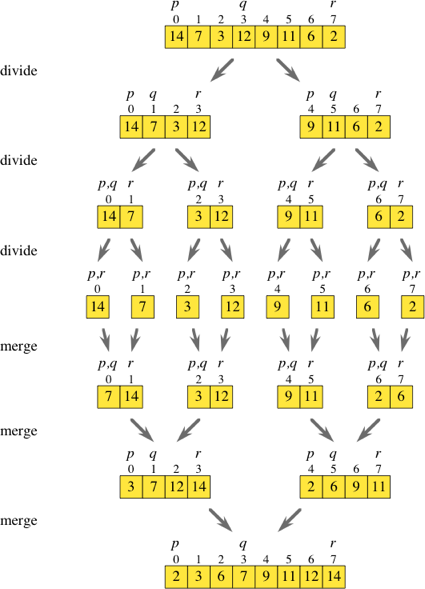
Ordenar fusión

Por lo tanto, combinar sort es un algoritmo de divide y vencerás. Mientras miraba el diagrama anterior, pensaba si era posible omitir básicamente todos los pasos de división.

Si iteraba sobre la matriz original mientras saltaba por dos, podría obtener los elementos en el índice i e i + 1 y colocarlos en sus propias matrices ordenadas. Una vez que tenga todas estas sub-matrices ([7,14], [3,12], [9,11] y [2,6] como se muestra en el diagrama), simplemente puede continuar con la rutina normal de fusión para obtener Una matriz ordenada.

¿La iteración a través de la matriz y la generación inmediata de las sub-matrices requeridas es menos eficiente que realizar los pasos de división en su totalidad?

— Jimmy_Rustle
fuente

Relacionado: cs.stackexchange.com/questions/77075/…

— Omar

Respuestas:

La confusión surge de la diferencia entre la descripción conceptual del algoritmo y su implementación .

La ordenación de fusión lógica se describe como dividir la matriz en matrices más pequeñas y luego fusionarlas nuevamente. Sin embargo, "dividir la matriz" no implica "crear una matriz completamente nueva en la memoria", ni nada de eso, podría implementarse en código como

/*
 * Note: array is now split into  [0..n) and [n..N)
 */

es decir, no se realiza ningún trabajo real, y la "división" es puramente conceptual. Entonces, lo que sugiere ciertamente funciona, pero lógicamente todavía está "dividiendo" las matrices, simplemente no necesita ningún trabajo de la computadora para hacerlo :-)

— psmears
fuente

Personalmente, me gusta mucho el tipo de fusión de abajo hacia arriba porque es más simple de implementar de una manera que le permite evitar asignar un búfer temporal en cada nivel de recursión. En su lugar, asigna un búfer una vez y hace ping-pong entre ellos.

— Ratchet Freak

Esto: dividir es computacionalmente un no-op ... más la sugerencia de OPs es solo una introducción de un equivalente a una fusión de matrices de elementos individuales, y comenzar a usar la fusión desde el segundo paso, lo que parece redundante, porque la fusión original funciona igual de bien. No tiene sentido optimizar eso. Solo introduce conceptos y lógica redundantes.

— luk32

@ratchetfreak: a mí también me encanta, pero lamentablemente no es equivalente a un top-down (al menos la versión que conozco). Combinará de manera diferente, básicamente redondeando a la siguiente longitud de matriz de potencia de 2, que creo que incluso podría ser un poco más lenta. ¿Conoces una versión de abajo hacia arriba que haga exactamente las mismas fusiones sin pagar un alto costo en otro lugar?

— user541686

@Mehrdad, el único problema real es la pequeña cola que debe fusionarse. En el peor de los casos, eso significa otro pase para fusionar en un solo elemento para conjuntos de longitud 1<<n+1. Aunque estoy seguro de que puedes ajustar las cosas para que una cola demasiado pequeña se fusione en un pase más bajo.

— monstruo de trinquete

@psmears "simplemente no necesitas ningún trabajo de la computadora para hacerlo", ¿entonces supongo que el costo de rendimiento de n llamadas de alguna función de división recursiva (7 llamadas en el diagrama de ejemplo) es básicamente insignificante?

— Jimmy_Rustle

Supongo que lo que quieres decir es la implementación de abajo hacia arriba . En la implementación de abajo hacia arriba, comienza a partir de elementos de celda única y avanza fusionando elementos en listas / matrices ordenadas más grandes. Simplemente invierta las flechas en su figura anterior comenzando desde la matriz del medio, es decir, matrices de un elemento.

Además, es posible que desee optimizar el tipo de fusión por dividiendo las matrices hasta que alcancen un tamaño constante, después de lo cual simplemente las ordena utilizando, por ejemplo, la ordenación por inserción.

De lo contrario, no es posible ordenar sin dividir la matriz. De hecho, la esencia del tipo de fusión es dividir y clasificar subarreglos, es decir, dividir y conquistar.

— fade2black
fuente