El problema se puede resolver en O (polylog (b)).
Definimos f(d, n)como el número de enteros de hasta d dígitos decimales con una suma de dígitos menor o igual a n. Se puede ver que esta función viene dada por la fórmula

Derivemos esta función, comenzando con algo más simple.
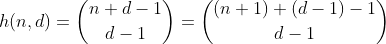
La función h cuenta el número de formas de elegir d - 1 elementos de un conjunto múltiple que contiene n + 1 elementos diferentes. También es la cantidad de formas de dividir n en d bins, que se pueden ver fácilmente construyendo d - 1 cercas alrededor de n ones y resumiendo cada sección separada. Ejemplo para n = 2, d = 3 ':
3-choose-2 fences number
-----------------------------------
11 ||11 002
12 |1|1 011
13 |11| 020
22 1||1 101
23 1|1| 110
33 11|| 200
Entonces, h cuenta todos los números que tienen una suma de dígitos de n y d dígitos. Excepto que solo funciona para n menos de 10, ya que los dígitos están limitados a 0 - 9. Para arreglar esto para los valores 10-19, necesitamos restar el número de particiones que tienen un bin con un número mayor que 9, lo que llamaré bins desbordados de ahora en adelante.
Este término puede calcularse reutilizando h de la siguiente manera. Contamos el número de formas de particionar n - 10, y luego elegimos uno de los contenedores para colocar el 10, lo que resulta en el número de particiones que tienen un contenedor desbordado. El resultado es la siguiente función preliminar.
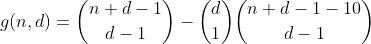
Continuamos de esta manera durante n menos o igual a 29, contando todas las formas de dividir n - 20, luego seleccionando 2 contenedores en los que colocamos los 10, contando así el número de particiones que contienen 2 contenedores desbordados.
Pero en este punto tenemos que tener cuidado, porque ya contamos las particiones que tienen 2 contenedores desbordados en el término anterior. No solo eso, sino que los contamos dos veces. Usemos un ejemplo y observemos la partición (10,0,11) con la suma 21. En el término anterior, restamos 10, calculamos todas las particiones de los 11 restantes y colocamos el 10 en uno de los 3 contenedores. Pero esta partición particular se puede alcanzar de una de dos maneras:
(10, 0, 1) => (10, 0, 11)
(0, 0, 11) => (10, 0, 11)
Como también contamos estas particiones una vez en el primer término, el recuento total de particiones con 2 contenedores desbordados asciende a 1 - 2 = -1, por lo que debemos contarlos una vez más agregando el siguiente término.
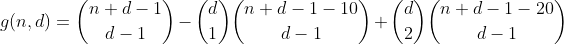
Pensando un poco más en esto, pronto descubrimos que la siguiente tabla puede expresar la cantidad de veces que una partición con un número específico de contenedores desbordados se puede expresar en la siguiente tabla (la columna i representa el término i, la fila j particiones con j desbordado contenedores).
1 0 0 0 0 0 . .
1 1 0 0 0 0 . .
1 2 1 0 0 0 . .
1 4 6 4 1 0 . .
. . . . . .
. . . . . .
Sí, es el triángulo de Pascal. El único recuento que nos interesa es el de la primera fila / columna, es decir, el número de particiones con cero contenedores desbordados. Y dado que la suma alterna de cada fila pero la primera es igual a 0 (por ejemplo, 1 - 4 + 6 - 4 + 1 = 0), así es como nos deshacemos de ellas y llegamos a la penúltima fórmula.
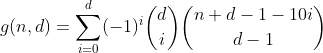
Esta función cuenta todos los números con d dígitos que tienen una suma de dígitos de n.
Ahora, ¿qué pasa con los números con suma de dígitos menor que n? Podemos usar una recurrencia estándar para binomios más un argumento inductivo, para mostrar que
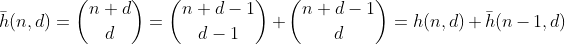
cuenta el número de particiones con suma de dígitos como máximo n. Y de esto se puede derivar f usando los mismos argumentos que para g.
Con esta fórmula, por ejemplo, podemos encontrar el número de números pesados en el intervalo de 8000 a 8999 1000 - f(3, 20), ya que hay miles de números en este intervalo, y tenemos que restar el número de números con una suma de dígitos menor o igual a 28 mientras se cuenta que el primer dígito ya contribuye 8 a la suma de dígitos.
Como un ejemplo más complejo, veamos el número de números pesados en el intervalo 1234..5678. Primero podemos pasar de 1234 a 1240 en pasos de 1. Luego pasamos de 1240 a 1300 en pasos de 10. La fórmula anterior nos da la cantidad de números pesados en cada intervalo:
1240..1249: 10 - f(1, 28 - (1+2+4))
1250..1259: 10 - f(1, 28 - (1+2+5))
1260..1269: 10 - f(1, 28 - (1+2+6))
1270..1279: 10 - f(1, 28 - (1+2+7))
1280..1289: 10 - f(1, 28 - (1+2+8))
1290..1299: 10 - f(1, 28 - (1+2+9))
Ahora vamos de 1300 a 2000 en pasos de 100:
1300..1399: 100 - f(2, 28 - (1+3))
1400..1499: 100 - f(2, 28 - (1+4))
1500..1599: 100 - f(2, 28 - (1+5))
1600..1699: 100 - f(2, 28 - (1+6))
1700..1799: 100 - f(2, 28 - (1+7))
1800..1899: 100 - f(2, 28 - (1+8))
1900..1999: 100 - f(2, 28 - (1+9))
De 2000 a 5000 en pasos de 1000:
2000..2999: 1000 - f(3, 28 - 2)
3000..3999: 1000 - f(3, 28 - 3)
4000..4999: 1000 - f(3, 28 - 4)
Ahora tenemos que reducir el tamaño del paso nuevamente, pasando de 5000 a 5600 en pasos de 100, de 5600 a 5670 en pasos de 10 y finalmente de 5670 a 5678 en pasos de 1.
Un ejemplo de implementación de Python (que recibió ligeras optimizaciones y pruebas mientras tanto):
def binomial(n, k):
if k < 0 or k > n:
return 0
result = 1
for i in range(k):
result *= n - i
result //= i + 1
return result
binomial_lut = [
[1],
[1, -1],
[1, -2, 1],
[1, -3, 3, -1],
[1, -4, 6, -4, 1],
[1, -5, 10, -10, 5, -1],
[1, -6, 15, -20, 15, -6, 1],
[1, -7, 21, -35, 35, -21, 7, -1],
[1, -8, 28, -56, 70, -56, 28, -8, 1],
[1, -9, 36, -84, 126, -126, 84, -36, 9, -1]]
def f(d, n):
return sum(binomial_lut[d][i] * binomial(n + d - 10*i, d)
for i in range(d + 1))
def digits(i):
d = map(int, str(i))
d.reverse()
return d
def heavy(a, b):
b += 1
a_digits = digits(a)
b_digits = digits(b)
a_digits = a_digits + [0] * (len(b_digits) - len(a_digits))
max_digits = next(i for i in range(len(a_digits) - 1, -1, -1)
if a_digits[i] != b_digits[i])
a_digits = digits(a)
count = 0
digit = 0
while digit < max_digits:
while a_digits[digit] == 0:
digit += 1
inc = 10 ** digit
for i in range(10 - a_digits[digit]):
if a + inc > b:
break
count += inc - f(digit, 7 * len(a_digits) - sum(a_digits))
a += inc
a_digits = digits(a)
while a < b:
while digit and a_digits[digit] == b_digits[digit]:
digit -= 1
inc = 10 ** digit
for i in range(b_digits[digit] - a_digits[digit]):
count += inc - f(digit, 7 * len(a_digits) - sum(a_digits))
a += inc
a_digits = digits(a)
return count
Editar : reemplazó el código por una versión optimizada (que se ve aún más fea que el código original). También arreglé algunos casos de esquina mientras estaba en eso. heavy(1234, 100000000)toma alrededor de un milisegundo en mi máquina.
