Si vivieras al otro lado de la Luna, ¿cómo podrías inferir la existencia de la Tierra?

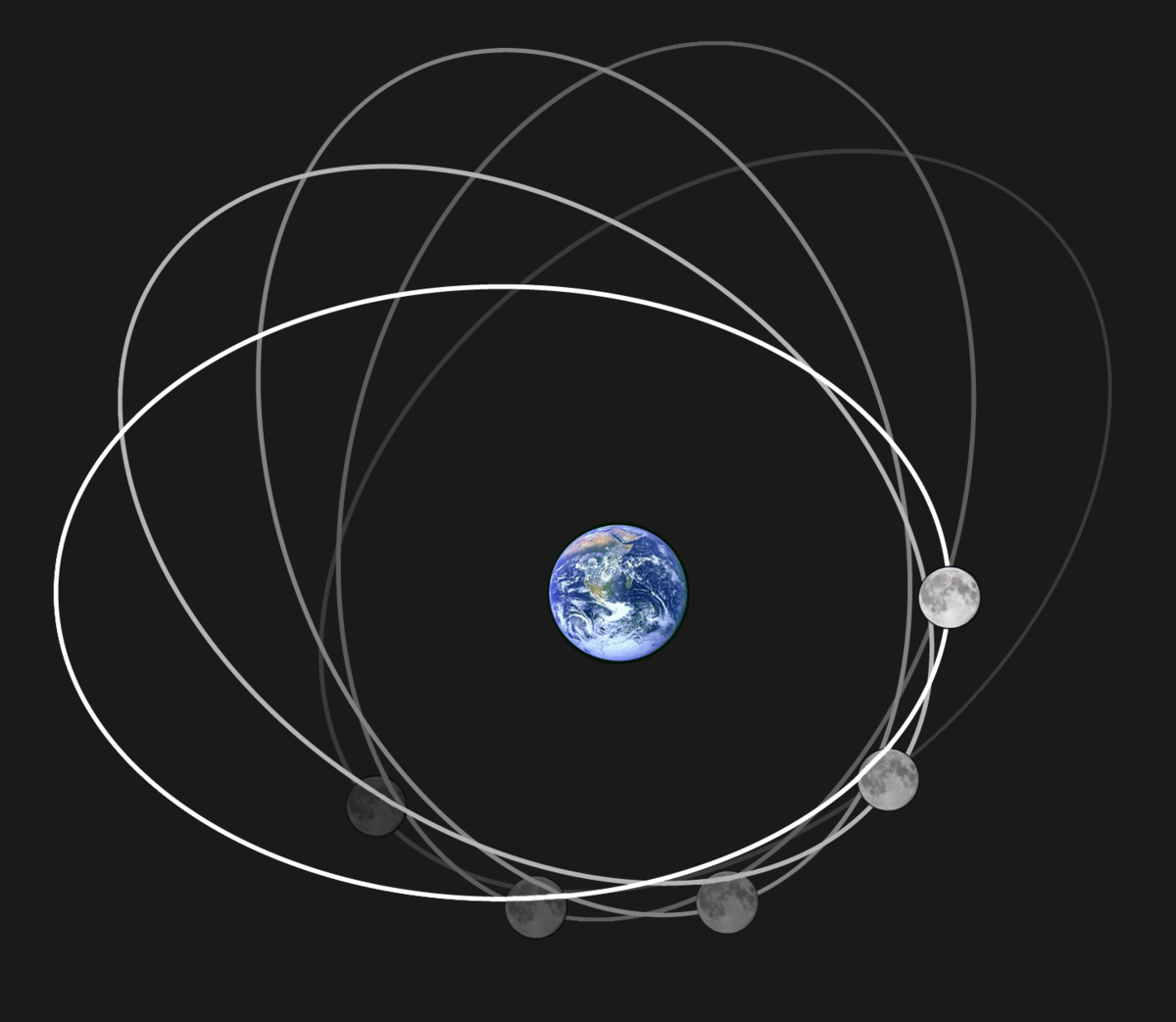
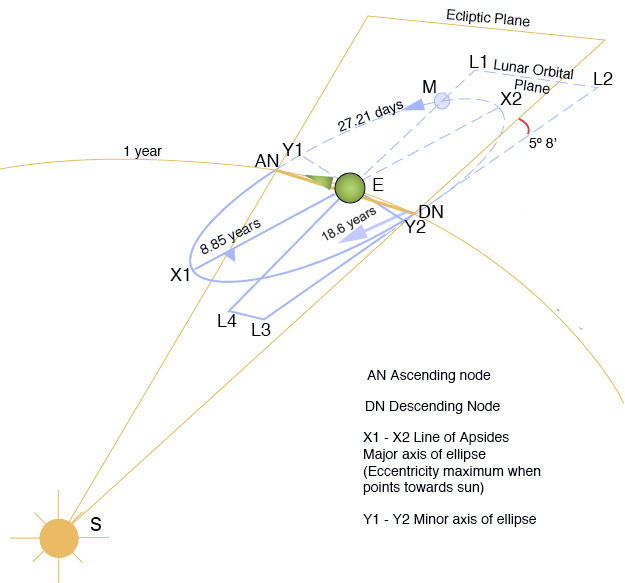
Supongamos que deposita a un astrónomo, armado con nuestro conocimiento actual de la mecánica orbital, en una cúpula en el lado opuesto de la Luna, de modo que la Tierra esté perpetuamente oculta para ellos.

(Y, por supuesto, suponga que esta persona no tiene un conocimiento específico sobre el sistema en el que se encuentra más allá de lo que puede obtener de las observaciones. Si lo desea, imagine que aprendió toda nuestra mecánica orbital moderna y física relacionada en alfa centauri, y luego me teletransportaron a nuestra Luna.)

Ahora, es razonable esperar que esta persona pueda deducir de las observaciones del cielo que el cuerpo en el que se encuentra es la mitad de un sistema binario, y debería poder medir las características orbitales (eje semi-mayor, elipticidad, inclinación), así como la posición del baricentro (mucho más cerca del otro cuerpo, que corresponde a una pareja mucho más masiva). ¿Qué observaciones son necesarias para deducir esto? ¿Qué nivel de precisión de observación se necesita para esas observaciones y a qué época histórica corresponde? (¿Sería suficiente el kit de Tycho Brahe? ¿Sería el de Galileo? ¿Serían los antiguos griegos? ¿O esto requeriría un observatorio de finales del siglo XIX (o incluso más tarde)?)

(Como se señaló en la respuesta de MartinV, nuestro astrónomo podría tener dificultades para distinguir entre situaciones con un par en órbita frente a un solo cuerpo enorme. Por lo tanto, si es conveniente, puede suponer que, a través de incursiones cortas de ~ 100 km desde la cúpula, nuestro astrónomo es capaz de medir el radio lunar midiendo inclinaciones solares en diferentes puntos con distancias conocidas entre ellos, a la Erathostenes .

— Emilio Pisanty
fuente

El paralaje estelar definitivamente ayudaría mucho, y eso es del siglo XIX.

@ LucJ.Bourhis Paralaje Estelar, o al menos su componente principal, va con el radio orbital alrededor del Sol, y los componentes de la órbita lunar serían mucho más pequeños que eso, por lo que me parece una solución no obvia (y es no es obvio que las observaciones del siglo XIX harían la precisión necesaria, tampoco). Sospecho que el candidato más probable es la paralaje del Sol con el fondo estelar (o, de manera equivalente, las posiciones de las estrellas con un reloj sincronizado con el día lunar), pero me gustaría saber qué precisión (en comparación con las referencias históricas) Necesito eso.

— Emilio Pisanty

¡Seguro! Esto no es lo que tenía en mente. Históricamente, el hecho de que la Luna es observable desde la Tierra fue instrumental en la medición de la distancia Tierra-Sol de la que depende mucho afaiu. Estaba pensando en usar paralaje para controlar esa distancia.

Aún así, la paralaje de medio mes podría ser útil para algo como Marte. El diámetro orbital de la Luna es de ~ 0.0026 UA, Marte puede estar a ~ 1AU afuera, de modo que el ángulo es de ~ 0.0052 radianes o 0.3 grados, ¿no? No estoy seguro de cómo se comparan con las observaciones de paralaje estelar a lo largo de los años, pero parece que eso podría cambiar la posición de Marte en relación con las estrellas distantes de una manera observable.

Me pregunto si la inclinación de 5 grados de la Luna sería suficiente. (5,14 grados), que equivale a aproximadamente un 9% de su distancia orbital hacia arriba y hacia abajo cada 29 días) o 1/6 de 1 grado con respecto al sol. Relativo a Marte en pase cerrado, un poco menos. 14 días observando que Marte se mueve hacia arriba o hacia abajo, pero no de manera consistente, ya que, a veces hacia arriba, a veces hacia abajo, podría ser el más notable.

— userLTK

Respuestas:

UNA sismómetro de marea corporal en el lado lejano de la Luna captaría tanto la marea solar como la distorsión corporal de 20 pulgadas producida por la Tierra . Mientras está "bloqueada por la marea", la luna no está en una órbita perfectamente circular, y también se tambalea un poco; libración . Su sismómetro debería recoger ambos efectos.

Ver el ciclo de paralaje de Marte cada 28 días, como se sugiere en los comentarios anteriores, podría ser una forma más sencilla de hacerlo.

— Extraño caminante
fuente

Esta es una respuesta interesante. De hecho, la Tierra elevará una pequeña "marea" en la Luna y la libración hará que se mueva. El efecto es pequeño y sutil: por sí solo, ¿permitiría a un científico inteligente deducir la existencia de un cuerpo desconocido e invisible en el espacio?

— MartinV

Los efectos sísmicos son interesantes, aunque no está claro para mí cómo podría medirlos. Y sí, estoy de acuerdo en que el paralaje es la respuesta más probable, pero estaba buscando algo más cuantitativo y detallado.

— Emilio Pisanty

Esta es una muy buena pregunta, y bastante sutil.

TL; DR;

La primera oportunidad podría ser que los cambios entre meses en la paralaje estelar del Sol podrían llevar al observador a concluir que i) la Luna es un cuerpo giratorio único, muy grande o ii) es parte de un co-cuerpo de varios cuerpos. sistema rotativo. Sin embargo, i) parecería ser inconsistente con un horizonte cercano y fuertemente curvado.

Si no es así, ciertamente cuando desarrollamos un modelo cuantitativo de mecánica orbital que involucra masa y gravedad

No creo que la paralaje estelar nos ayude directamente, ya que (en la actualidad) simplemente nos dice que estamos en órbita alrededor del sol y poco sobre el sistema Tierra-Luna.

Veamos cómo podría verlo un equivalente de Ptolomeo en la Luna (llámelo Luna-Ptolomeo). No tendría forma de distinguir el sistema Tierra-Luna de su suposición de que solo está sentado en un objeto sólido en el centro de la creación. Por supuesto, no vería una "luna" en órbita a su alrededor, pero sí vería el Sol, las estrellas y los planetas principales. Paralaje estelar (para él, el Sol "moviéndose a través del Zodiaco) simplemente le diría que el Sol está girando alrededor de su Luna, al igual que los planetas. La existencia de epiciclos planetarios sería una curiosidad necesaria para que su modelo funcione, pero lo hace trabaja y no tiene noción de la Tierra

Moon-Galileo podría (o no) ser capaz de desarrollar el modelo heliocéntrico: se pierde una idea clave que tenía Earth-Galileo: que la Tierra no era especial porque otros planetas también tenían lunas. Moon-Galileo encontraría interesante el sistema orbital de Júpiter, pero no una idea clave, por lo que podría no desarrollar el nuevo modelo. Aun así, alguien más lo haría.

Sin embargo, en un mundo científico cualitativo, todavía no habría nada para ayudar al observador de la Luna a deducir la existencia de la Tierra detrás del horizonte.

Sospecho que la verdad se volvería inevitable cuando la mecánica orbital se desarrollara lo suficiente como para incorporar la masa y la gravedad en el cálculo. Pudo haber sido en la época de Moon-Kepler.

No estoy seguro de estar de acuerdo con los comentarios que miran las observaciones de los planetas; no veo cómo ayudan a distinguir entre un sistema Tierra-Luna en lugar de un cuerpo lunar simple, muy grande y giratorio sin coorbitador ( lo cual sería una suposición natural hacer). Incluso los cambios mensuales en el paralaje causados por la rotación de la Luna alrededor de la Tierra podrían evitarse sugiriendo la rotación simple de un cuerpo de la Luna mucho más grande, aunque nuestro héroe ciertamente podría cuestionar la compatibilidad de esto con la curvatura aparente y la distancia a su Horizonte lunar

— MartinV
fuente

Parece que he comunicado mal la intención de la pregunta. Puede asumir un conocimiento moderno completo de la mecánica orbital si es necesario ─ al hacer comparaciones históricas, estoy interesado principalmente en la técnica experimental, no en los avances conceptuales. Si lo desea, puede pensar en la situación como un astrónomo que aprendió toda la mecánica orbital moderna en alfa centauri y luego se teletransportó a la superficie de nuestra Luna. Entonces, tienen pleno conocimiento de cómo funcionan la gravedad y la mecánica, simplemente no tienen ningún conocimiento previo a la observación del sistema específico en el que se encuentran.

— Emilio Pisanty

Pero en lo que respecta a tu Ptolomeo lunar, ¿no necesitaría incluir un epiciclo para el sol? Esa es la observación de paralaje estelar que se traduciría al radio orbital Tierra-Luna una vez que cambies a una perspectiva heliocéntrica. Pero, ¿qué tan importante sería y qué tan difícil sería medir?

— Emilio Pisanty

Gracias Emilio, en el epiciclo solar, creo que probablemente sería demasiado pequeño dado el equipo disponible para Moon-Ptolemy. En su otro comentario, no hay falta de comunicación en absoluto; fue tu pregunta, ¡así que creo que no entendí bien! Dado un experto con equipo moderno trasplantado a la Luna, creo que lo resolverían bastante rápido: una combinación de las oscilaciones en paralaje combinado con el tamaño aparente de la Luna sin duda plantearía la cuestión. De hecho, el experto miraría la pequeña Luna rocosa en sí misma y de inmediato haría la pregunta "¿qué es esta órbita alrededor?"

— MartinV

Sí, mi expectativa es que lo resolverían bastante rápido; la pregunta era cómo y qué equipo necesitarían. (En su última oración, no creo que sea una pre-expectativa natural, dado lo poco que sabemos de la prevalencia de los exoplanetas rocosos. Pero con solo mirar la superficie, las diferencias entre la Luna y Ceres son mínimas , por lo que la superficie no necesariamente sugiere que estás en un satélite. En cambio, dado el radio y la gravedad de la superficie, la superficie rocosa y la falta de atmósfera podrían ser características bastante naturales.)

— Emilio Pisanty

Un observador en el otro lado de la luna tendría dificultades para explicar que se encuentra en un solo planeta, debido al movimiento de la cosa más notable en el cielo: ¡el sol!

De hecho, debido a la excentricidad de la órbita de la luna alrededor de la Tierra, la duración del día, es decir, la "velocidad en el cielo" del sol, depende de dónde se encuentre en su órbita lunar.

Y a partir de las observaciones que puede hacer, por ejemplo, otros planetas que son casi perfectamente redondos en el sistema solar (y por razones bien conocidas), debería verse obligada a descartar la hipótesis "Estoy parado en un cuerpo celeste elíptico único".

No puedo calcular la variación de la duración del día en el lado opuesto de la luna en un período de tiempo razonable, lo siento.

Otro efecto que trataré de ilustrar con imágenes de Wikipedia: la elevación de la trayectoria del sol en el cielo cambiaría año tras año (ciclo: entre 8 y 9 años terrestres), debido a la precesión absidal de la luna y su plan de órbita inclinada:

Por Rfassbind - Trabajo propio., Dominio público, Enlace

Por Geologician, Homunculus 2 - de Wikipedia en inglés, CC BY 3.0 , Enlace

— J. Chomel
fuente